This post describes how to calculate a confidence interval on a sample set of more than 30 observations. For this example let’s start out with some data of number of e-commerce orders by country (Germany in this case).
In this example we’re going to use a 95% confidence interval (CI) that allows us to say something along the lines of “with 95% confidence we can predict that we will see between x and y number of orders coming in from Germany tomorrow”. To start out i’ve organized the values with two columns (date and country).
To start calculating the confidence interval, I’m gonna start filling out a bunch of values in some column to the left of the table, E or F for example. Let’s say my table is named Orders and the column containing order quantity for Germany is called GERMANY, then I will get down the following (using column F):
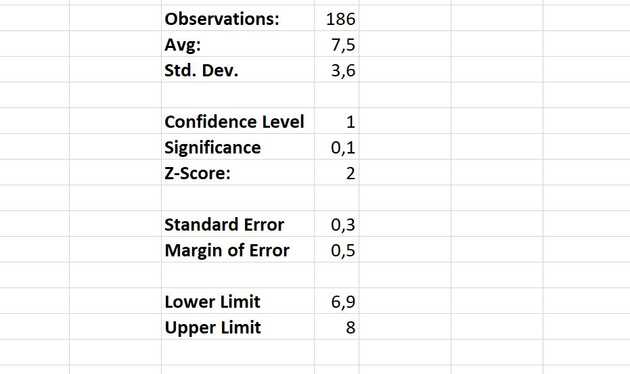
- Number of observations (=COUNT(Orders[GERMANY]))
- Average (=AVERAGE(Orders[GERMANY]))
- Standard Deviation (=STDEV.S(Orders[GERMANY])
- Confidence Level - for a 95% confidence level this means 0.95
- Significance: (1 - Confidence level), ie. 0.05 (=1-F6 )
- Z-Score: The number of standard deviations from the average where a value is located. In this case we’re looking for the z-score within which 95% of the values lie, +/- the number of standard deviations from the mean (=ABS(NORM.S.INV(F7/2))). Absolute values are easier to deal with which is why the ABS function is used.
- Standard error - calculated by dividing the standard deviation by the square root of the number of measurements (=F4/(SQRT(F2))). Ie. the expected error expected to occur per standard deviation.
- Margin of error - the z-score multiplied by the standard error
- Lower Limit - Now we can solve for the lower limit which is the same as the sample mean - the margin of error
- Upper Limit - the sample mean - the margin of error
In other the words the 95% confidence interval lies in the range of 6.9 - 8, which is to say we can, with 95% confidence expect 6.9 - 8 orders from Germany any given day.